Hace unos meses, en Factor Finanzas realizamos un artículo sobre las opciones, explicando de forma general en qué consisten y porqué se utilizan. Hoy en este artículo entraremos en el detalle de uno de los modelos de valoración más conocidos, el binomial, además de ejemplificar su uso con un ejemplo práctico.
Recapitulando sobre el artículo introductorio, llegamos a la conclusión que una opción es un instrumento que, al comprarlo, da el derecho, pero no la obligación de ejercer el contrato (opción), esto quiere decir que el inversionista decidirá si desea hacer efectivo el pago de este.
La ejecución del contrato dependerá de su valor, que en seguida explicaremos.
¿Comó valorar una opción?
Existen distintos métodos para conocer cuál es el valor de una opción, hoy analizaremos el modelo binomial, que permite valorizar una gran cantidad de tipo de opciones, dentro de las que están la de tipo europea (solo se puede ejercer al final del contrato) o americana (en cualquier momento del contrato), aunque nos enfocaremos en el de tipo europeo para la explicación.

Modelo Binomial
El modelo binomial es utilizado para establecer el valor de la opción por medio de probabilidades de ocurrencia de un aumento o disminución del precio del activo subyacente, este precio aumentará o disminuirá en una proporción fija que se denomina “u” para la subida de precio y “d” para la caída de este.
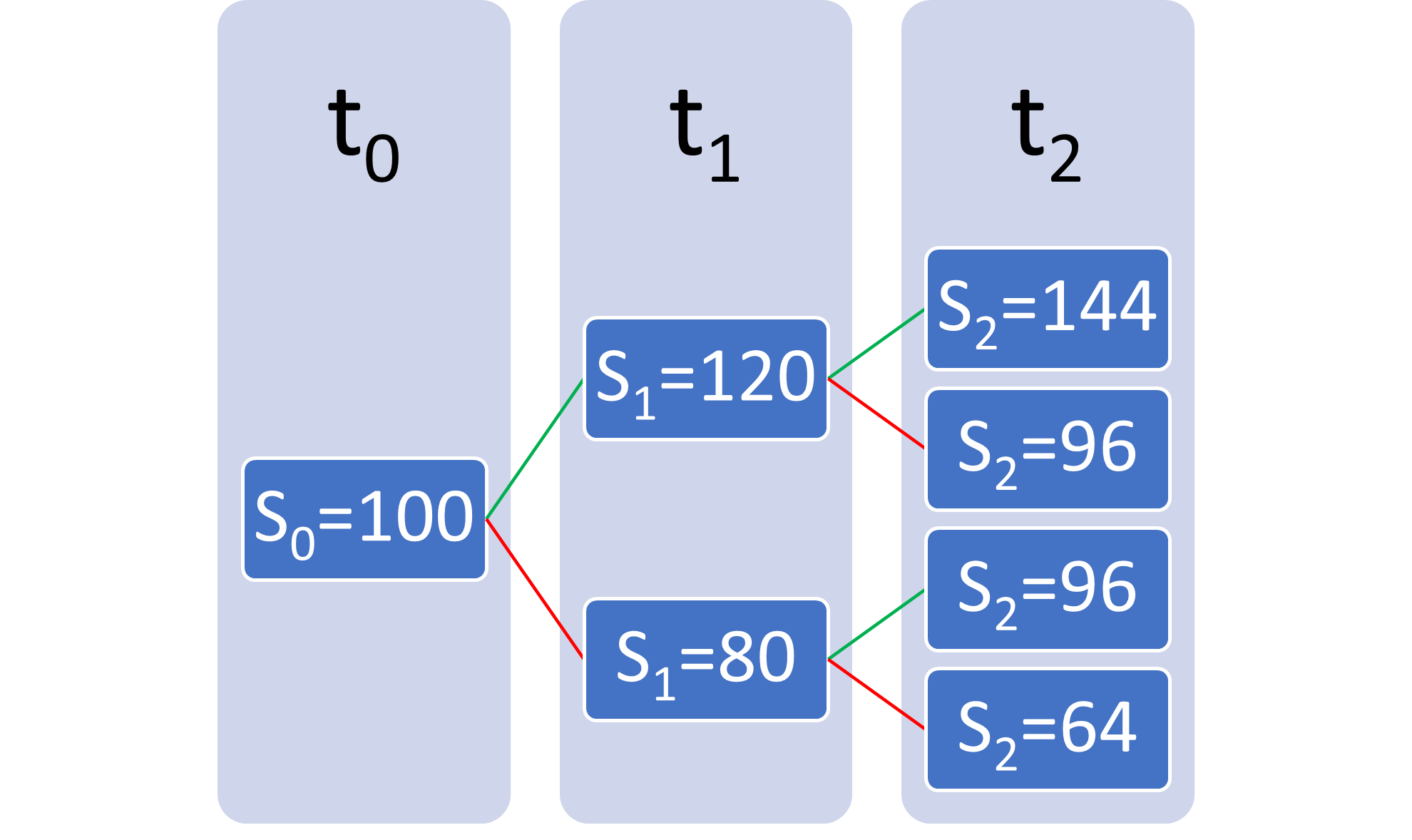
El precio del subyacente (activo sobre el que se ejercerá la opción) se denomina con la letra Si donde i representa el tiempo, siendo S1 el precio del activo subyacente en el periodo 1.
Para representar el modelo de forma visual, usaremos un “árbol”, que nos permitirá observar los distintos caminos que puede tomar el precio del subyacente como el de la opción, primero dibujaremos el árbol para el precio del subyacente, y luego el del precio de la opción, ya que, para poder hacer el segundo, necesitaremos la información del primero.
En el dibujo representaremos las subidas de precio del subyacente con líneas verdes, mientras que las caídas en rojo.
Opción Call
Supongamos que analizamos la compra de una opción call (derecho a compra del subyacente) con un precio de ejercicio de 110 en t2, esto quiere decir que tendrá el derecho a comprar el subyacente a 110 en el periodo t2.
El pago de una opción call es igual a Si-K, donde Si es el precio del subyacente en el periodo de tiempo i, mientras que K es el precio de ejercicio de la opción call, que en este caso es 110. Hay que tener en cuenta que el pago de la opción no podrá ser negativo, ya que el contrato da el derecho a ejercerlo, pero no la obligación, por lo que, si el valor fuera negativo, simplemente no se usaría el contrato y el pago seria 0
Con esto podemos calcular el valor de la opción en cada una de las ramificaciones del árbol, y después hacer una inducción hacia atrás, que es un proceso en el que se obtiene el valor de la opción en el periodo anterior dado los valores ya obtenidos al final del contrato, así sucesivamente hasta llegar al valor en la actualidad (t0)
La probabilidad de que el precio suba (p) o baje (1-p) dependerá de u, d y la tasa de interés libre de riesgo, siendo la probabilidad de \(p=\frac{{1+r-d}}{{u-d}}\)
En nuestro caso hemos asumido que:
- u=1,2
- d=0,8
- r=0
- S0=100
- K=110
Entonces podemos obtener la probabilidad de que aumente el precio
\(p=\frac{{1-0,8}}{{1,2-0,8}}=0,5\), o lo mismo que 50%.
Con esto sabemos que la probabilidad de aumento del precio en un factor de 1,2 es de \(p=50\%\), mientras que la disminución en un factor de 0,8 es de \(1-p=1-0,5=50\%\).
Ahora es posible hacer inducción hacia atrás, sabemos que el pago de la opción call es S-K, por lo que nos podemos poner en cada situación y llegar al valor C0 o valor actual de la opción.
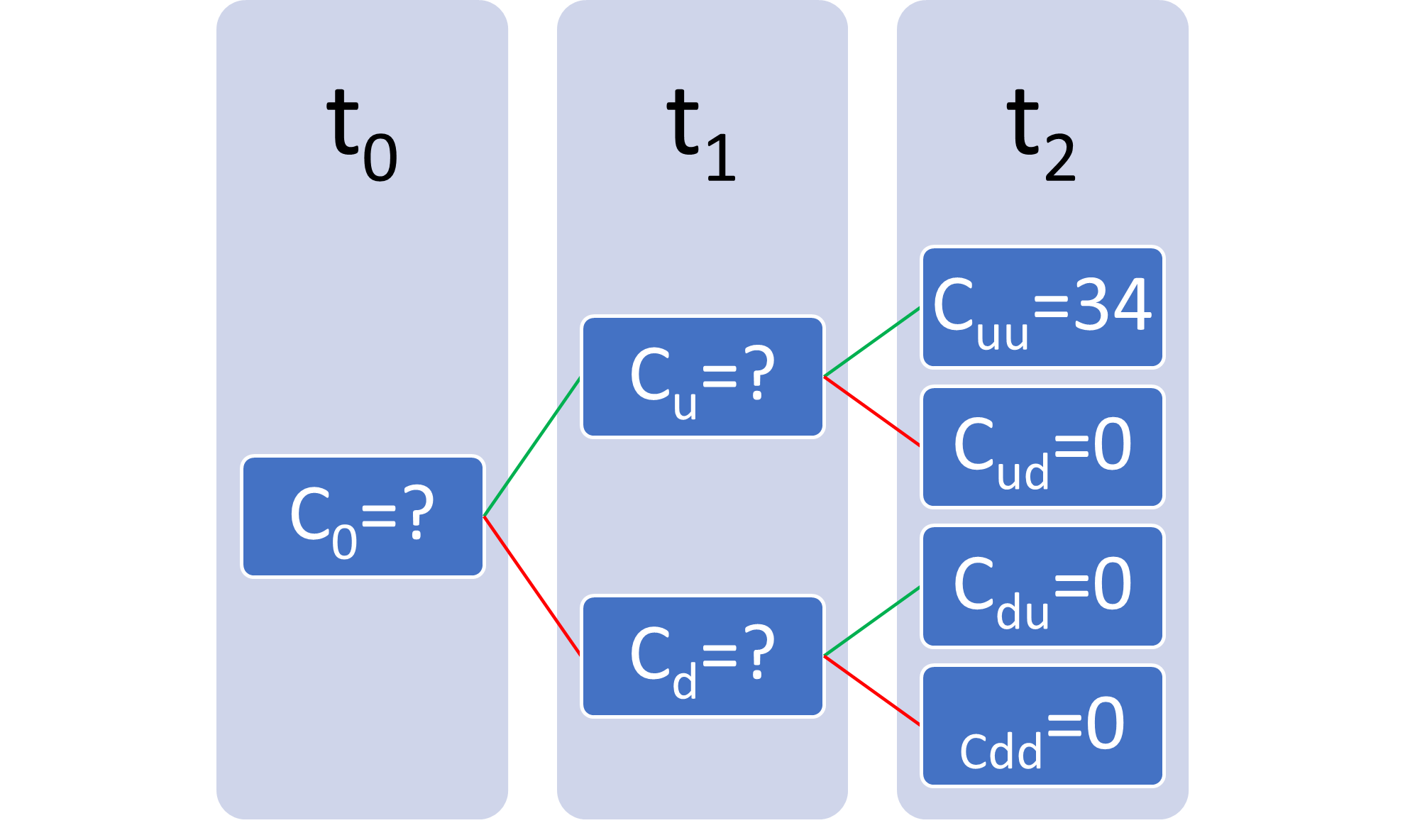
Ya tenemos todos los pagos en t2, para obtener los pagos de la opción en t1debemos obtener los pagos esperados de Cu y Cd, esto lo hacemos de la siguiente forma.
\({{C}_{u}}=\frac{{Cuu*p+Cud*\left( {1-p} \right)}}{{1+r}}\)
\({{C}_{u}}=\frac{{34*0,5+0*0,5}}{1}=17\)
\({{C}_{d}}=\frac{{Cdu*p+Cdd*\left( {1-p} \right)}}{{1+r}}\)
\({{C}_{d}}=\frac{{0*0,5+0*0,5}}{1}=0\)
Ahora tenemos Cu y Cd, por lo que podemos volver a aplicar la inducción hacia atrás para obtener C0.
\({{C}_{0}}=\frac{{Cu*p+Cd*\left( {1-p} \right)}}{{1+r}}\)
\({{C}_{0}}=\frac{{17*0,5+0*0,5}}{1}=8,5\)
Hemos logrado obtener el valor de C0, esto quiere decir que, si quisiéramos tener el derecho de comprar el subyacente a 110, deberíamos pagar 8,5 como máximo por el contrato.
Opción put
En el caso de la opción de venta (put) que es representada con la letra P, solo cambian los pagos de las opciones si mantenemos K=110, ya que en este tipo de contrato los pagos vendrán dados por K-S, lo que nos daría un árbol del siguiente estilo, con el que podríamos trabajar haciendo inducción hacia atrás como en el ejercicio de la opción de compra (call) anterior.
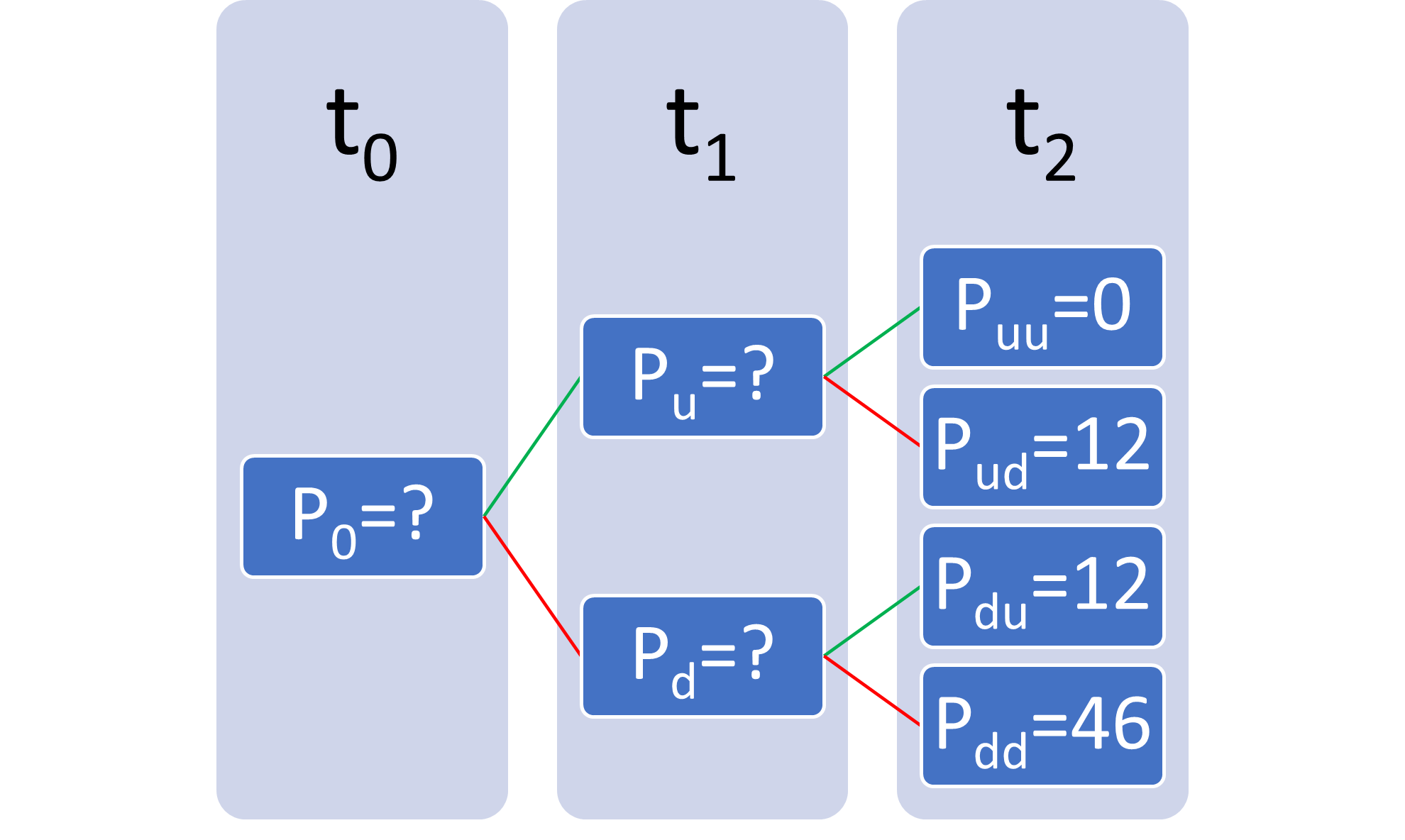
Resultando en:
\(Pu=\frac{{0*0,5+12*0,5}}{1}=6\)
\(Pd=\frac{{12*0,5+12*0,5}}{1}=6\)
\(P0=\frac{{6*0,5+6*0,5}}{1}=6\)
El valor de la opción de venta del subyacente a un precio de 110 en t2 vale 6 en la actualidad.